Dnn

第一章

• Representation Learning: Use machine to discover not only the mapping from representation to output but also the representation itself.（所以可以看出表示学习是机器学习的一个支线，它不仅学习输入到输出的关系，他还学习如何表示一个输入）
• Autoencoder:
  • encoder: converts the input data into a different representation
  • decoder: converts the new representation back to the original format
• 所以深度网络中的隐藏层可以被看作是负责特征提取的
• Two main ways of measuring the depth:
  • The first view is based on the number of sequential instructions that must be executed to evaluate the architecture
  • depth of the graph describing how concepts are related to each other
• 先留坑历史学习

应用数学与机器学习基础

线性代数

• 标量scalar：一个标量就是一个单独的数，它不同于线性代数中研究的其他 大部分对象(通常是多个数的数组)。我们用斜体表示标量。标量通常被赋予小写的变量名称。当我们介绍标量时，会明确它们是哪种类型的数。比如，在定义实数标量时，我们可能会说 ‘‘令 s ∈ R 表示一条线的斜率’’;在定义自然数标量时，我们可能会说 ‘‘令 n ∈ N 表示元素的数目’’。
• 向量vector：A vector is an array of numbers。一个向量是一列数。这些数是有序排列的。通过次序中的索 引，我们可以确定每个单独的数。通常我们赋予向量粗体的小写变量名称，比 如 x。向量中的元素可以通过带脚标的斜体表示。向量 x 的第一个元素是 x1，第二个元素是 x2，等等。所以在这里的向量特指的是一个[x1, x2, x3…, xn]这样的一个东西，所谓的“多维向量”其实都是张量。标准的向量都是列向量
• 矩阵matrix：矩阵特指一个二维数组，一个元素被两个索引而确定，这里的矩阵特指的是像2*2的矩阵
• 张量：超过二维的数组。就是各种各样奇形怪状的矩阵都用张量来表示比如（2*2*2）这就是一个三维的张量，就像是个立方体的一样
• 有时，我们通过将向量元素作为行矩阵写在文本行中，然后使用转置操作将其变为标准的列向量
• 在机器学习中，允许矩阵和向量相加，矩阵和向量相加的操作就像\( C = A_{i, j} + b_{j} \)，这个的意义是向量b和矩阵A的每一行（j）相加
• 这个简写方法使我们无需在加法操作前定义一个将向量 b 复制 到每一行而生成的矩阵。这种隐式地复制向量 b 到很多位置的方式，被称为 广播(broadcasting)。
• 矩阵和向量相乘：\( C_{i, j} = \sum_{k} A_{i, k}B_{k, j} \)
  • A(B + C) = AB + AC
  • A(BC) = (AB)C

• 单位矩阵(Identity Matrix)：比如说I_n，那他是个n*n的矩阵且在他的对角线上全都是1，其他位置全是0
• A的矩阵逆：\( A\times A^{-1} = I_{n} \)
• 并且通过证明可得：

Deep Feedforward Networks

• Deep feedforward networks, feedforward neural networks, Multilayer perceptrons其实都是一个东西。目的都是学的一个方程 \( f* \)比如可以用来学得一个把数据x映射到类别y的分类器。
• A feedforward network defines a mapping \( y = f(x;\theta) \) and learns the value of the parameters \( \theta \) that result in the best function approximation
• feedforward并没有feedback connection，有feedback connection的叫做recurrent network.
• 用数学的方式来表示layer：\( f(x) = f^{(3)}(f^{(2)}(f^{(1)}(x))) \)，那么可以看到在这个例子里面，
  • （1）就代表的是第一个layer
  • （2）代表的就是第二个layer。这个chain的长度就是模型的深度depth。
• 除了output layer，并没有额外的信息来告诉这个模型在每个hidden layer他应该如何表现
• 刚刚说到了depth深度，而hidden layer的维度则决定了模型的宽度
• It is best to think of feedforward networks as function approximation machines that are designed to achieve statistical generalization, occasionally drawing some insights from what we know about the brain, rather than as models of brain function

Linear Models

• Logistic regression，linear regression
• 使用他们的好处是：
  • Can be fit efficiently and reliably. either in closed form or with convex optimization
• 缺点就是线性模型只可以model线性函数，也就是说这种方式并不可以找出任何的关系
• 解决的办法是把数据x映射到\( \phi(x) \)，\( \phi(x) \)指的是x的一个新的representation，线性模型是可以作用在这个新的x上面
• 如何找到这个\( \phi () \)映射呢？
  • 把x映射到无限维，就像之前在自学452的时候说的那样
  • 手扒这个映射
  • 把这个\( \phi \)定义成一个hidden layer：\( y = f(x;\theta, w) = \phi(x;\theta)^{T} w \)。在这个方法下面，只需要先指明映射的大类，然后就可以让算法自己去学这个具体的映射(这是一个关于隐藏层的一个全新的理解)

6.1 Example: Learning XOR

• 数据集= {[0, 0], [0, 1], [1, 0], [1, 1]}

• 损失函数loss function：Mean Square Error：

  \[\begin{aligned} J(\theta) = \frac{1}{4} \sum_{x \in 数据集}(f^*(x) - f(x;\theta))^{2} \end{aligned}\]
• 所以在这些表示里面，\( \theta \)代表的是这一层级中的所有参数，那么在这里面的theta就有权重和bias，因为这个计算只是“一层的计算”。而像刚刚\( y = f(x;\theta, w) = \phi(x;\theta)^{T} w \)这个下面，为什么不把theta和w分在一起的原因是因为theta是属于那个映射的参数，而w是属于映射好了之后线性映射的参数，所以是不一样的

• 不管怎么说，现在的模型如下：

  \[\begin{aligned} & f(x;w,b) = x^T w + b \end{aligned}\]
• 这篇文章提出的一些看法是之前从来没讲过的，还是觉得把这么重要的一门课拿来给farhana这种划水教授讲真的败坏老子的前程。

• 下面两张图分别代表了现在的problem space和他propose的多层前置网络

  

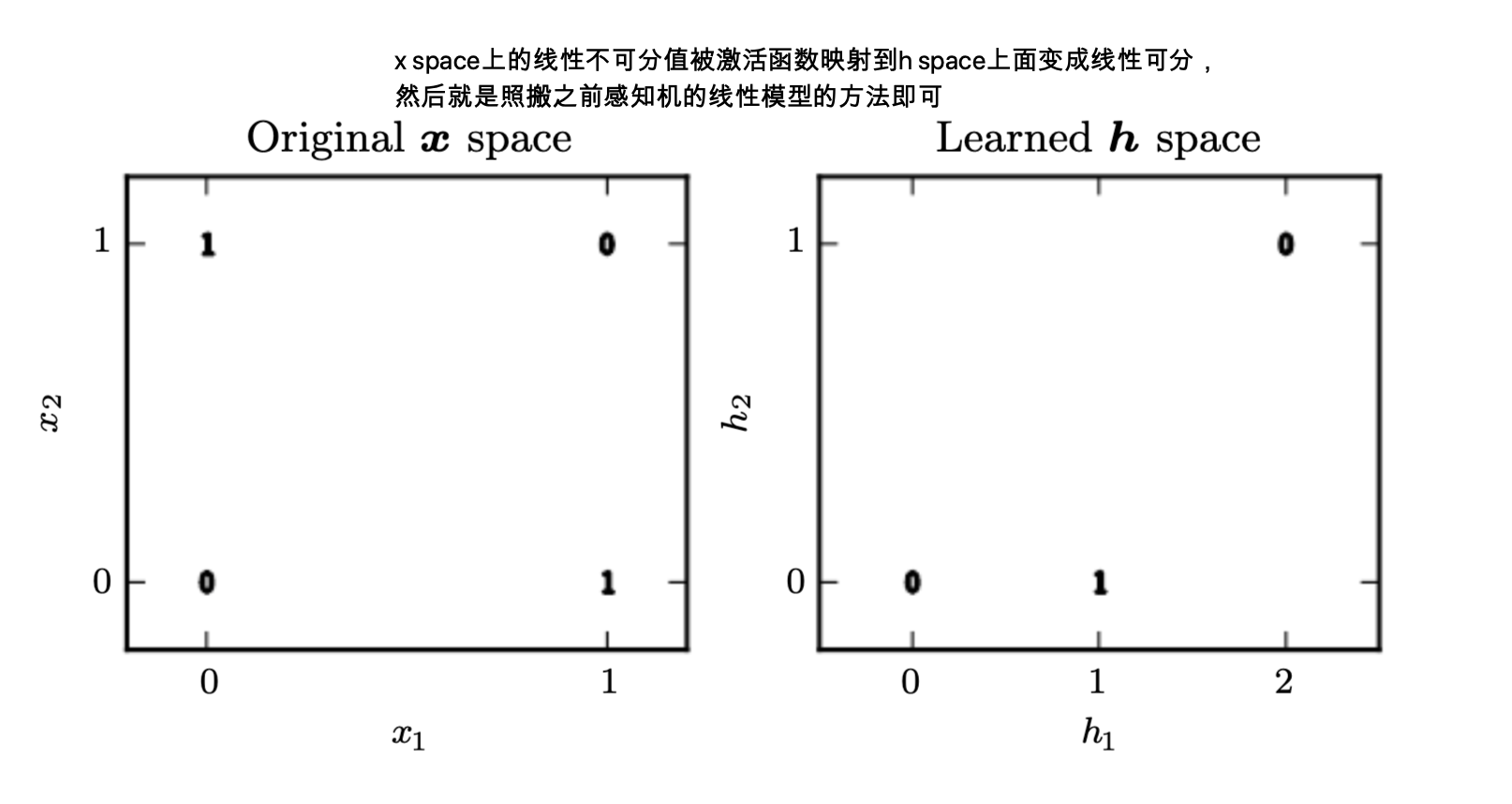
  • 观察右边的h sapce，他把(0, 1)和(1, 0)这两个点都映射到了同一个点(1, 0)上面，这样就线性可分了

  

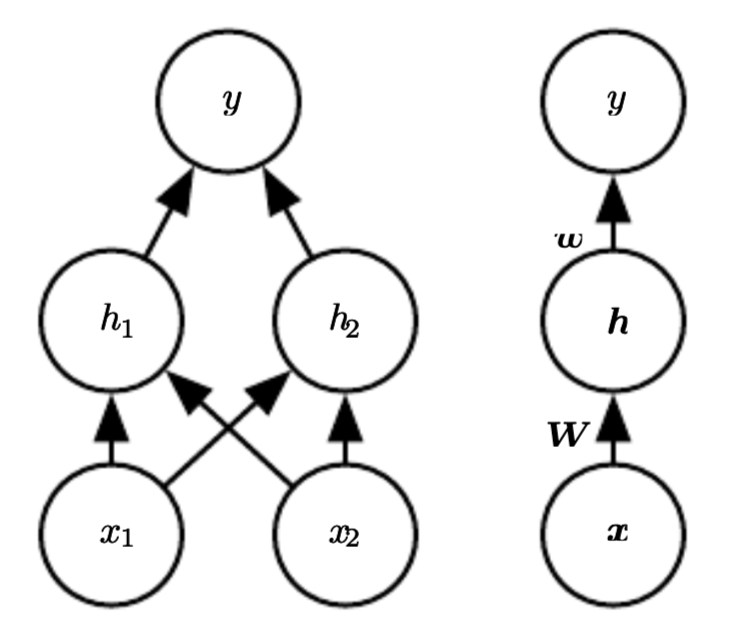
• 他这里关于激活函数的使用就和之前理解的很不一样。之前理解的是，激活函数表现的就像是神经元的携带信息的动作电位，而这里的解释是激活函数把线性不可分的数值等价的映射到线性可分的位置上面

• 隐藏层的激活函数选用线性函数的意义不大，如果隐藏层依然选用线性函数的话，整体的模型也还是一个线性函数

  \[\begin{aligned} & h = g(W^T x + c) \end{aligned}\]

• 以上的g代表的就是一个激活函数，在这里他选用的是ReLu（Rectified Linear Unit）线性整流函数（修正线性单元）

  \[f(x) = max(0, x)\]

• 那么这样整合下来的话，完整的模型就是:

  \[\begin{aligned} f(x;W, c, w, b) = w^{T} max(0, W^{T} x + c) + b \end{aligned}\]
• 书中还演示了一遍walk through，这个walkthrough是根据一个已有的答案来的，这个答案属于global minimum of loss function set里面，也就是说还有别的答案

6.2 Gradient-Based Learning

• Convex and loss function: Popular loss functions are convex because a local minimum of a convex function is a global minimum. 对于一个convex的loss function来说，我们的目标是找到这个loss function的convex的local minimum，这个local minimum只有一个且是global minimum。所以loss function如果是convex的话，对于之后找极值相当有帮助。
• 所以训练神经网络和线性模型最大的区别就是：
  • 线性模型使用convex optimization凸优化，而凸优化从任何initial parameters开始，只要找到了一局部最优，因为我们的损失函数是凸函数，那么也就找到了这个函数的全剧最优，所以“一旦将一个实际问题表述为凸优化问题，大体上意味着相应问题已经得到彻底解决，这是非凸的优化问题所不具有的性质。”
  • 神经网络模型使用的是随机梯度下降，使用这个的原因是因为神经网络的损失函数往往是非凸函数，非凸函数就不存在局部最优必定等于全局最优，所以神经网络的优化器只可以随机开始于损失函数的一点，然后慢慢一步一步找全剧最优（沿着梯度找）
    • 梯度：梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。
    • 所以其实对于神经网络的优化器来说，initial condition还挺重要的
• the training algorithmis almost always based on using the gradient to descend the cost function in oneway or another.

6.2.1 Cost function

• Cost function一般是这样定义的：In most cases, our parametric model defines a distribution \( p(y | x;\theta) \) and we simply use the principle of maximum likelihood
• 对数似然函数的代价函数的基本过程：想办法定义概率分布函数，取这个概率分布函数的log然后找最佳参数匹配
• 使用最大似然法则提取出来的cost function符合这个原理：
  • 机器学习可以看作是给定数据x，我们要预测y，假设y服从某一种分布，那么机器学习就是想要学得这个分布的具体的参数，假设已知label y服从某一概率分布，通过最大似然函数找出令P(y | 参数)最大的参数值来确定概率模型的参数，这样子就是用最大似然函数去求代价函数的基本意义
  • Principle of maximum likelihood:

    • 简单来说就是我们选择模型是基于概率的：我们选择模型的原则是，他比所有别的模型都更好，给定样本的情况下，参数是某参数的概率是最高的，也就是参数基于样本的后验概率是最高的，以下是一个最大似然估计（Maximum Likelihood Estimation）的例子 假设有个袋子，里面有7个白球和三个红球，设白球的比例为\( \theta \)

      \[\begin{aligned} f(x_{1}, x_{2} | \theta) = f(x_{1}|\theta) \times f(x_2 | \theta) \end{aligned}\]

      其中x1和x2表示两次采样，f是模型而theta是模型的参数，因为这两个样本是独立同分布，所以他们一起发生的概率就是相乘在一起，现在模型参数theta是未知的，为了求得这个theta，我们把似然L定义成theta关于采样的后验概率

      \[\begin{aligned} L(\theta|x_1, x_2) = f(x_1, x_2 | \theta) = \prod_{i = 1}^{2} f(x_i | \theta) \end{aligned}\]
    • 所以接下来的目的，就是找到令似然函数最大的theta值
    • 一般来说，就是要找到这个最大值，甚至可以直接求导
• 像刚刚的例子他定义的分布就很简单就是一个概率分布，而在机器学习中，如果把似然和概率分布的概念利用起来的话，就可以得到下面的式子
• 其中，\( P_{model}(x;\theta) \)是：maps any configuration x to a real number estimating the true probabolity

• 然后\( P_{model}(x) \)也等同于p(y|x;theta) \(\begin{aligned} \theta_{ML} = argmax_{\theta} \prod_{i = 1}^{m} P_{model}(x^{(i)};\theta) \end{aligned}\)

• 意思就是给定参数和模型下面，预测出来的类别是这个y的概率是多少，那么为什么有的时候说log p呢，这是因为，如果两边同时取对数的话，不影响函数的单调性也不影响选出来的theta值，但可以把连乘变成连加，大大减少了之后求导的难度

• 所以我们训练theta值的时候这么训练的:

6.2.1.1 Learning Conditional Distributions with Maximum Likelihood

• 以上就是一个cost function，适用于各种模型，根据不同log p模型的选择，最终出来的cost function也不一样。打个比方如果是linear regression的话，他代入的结果就是一个mean suqare error cost
• 这个的好处是，因为需要用到梯度，我们的代价函数需要large and predictable enough才可以成为一个很好的指路人，求得的梯度才有意义。但是如果一些非常饱和的代价函数（饱和的代价函数指的是在图像上非常平的代价函数）会破坏这种算法，也不能说是破坏吧，总而言之就是会令算法的效率非常低并且可能会陷入局部最优。造成这一问题的原因是有些激活函数在遇到极负的参数会变得饱和：几个输出单元都涉及到一个exp函数，当它的参数非常负面时，这个函数可能会达到饱和。负对数似然代价函数中的对数函数抵消了某些输出单元的输出.
  • 这个抵消就很关键：\( Log_{e} e^{X} = X \)
• 对于实值输出变量，如果模型能够控制输出分布的密度(例如，通过学习高斯输出分布的变异参数)，那么就有可能将极高的密度分配给正确的训练集输出，从而导致交叉熵趋近于负无穷。第7章描述的正则化技术提供了几种修改学习问题的不同方法，这样模型就不能以这种方式获得无限的回报（完全没看懂的一句话）：极高的密度也就是说如果习得的参数是正确的话，那么模型就可以为这个参数匹配极高的概率，从而在接下来的梯度里面对其进行比较小的调整

6.2.1.2 Learning Conditional Statistics

• Instead of learning a full probability distribution \( p(y |x;\theta) \), we often want to learn just one conditional statistic of y given x. 比如，我们可能只想知道我们训练出来的y的平均值
• 这个东西就很牛逼，如果我们把神经网络理解成：神经网络可以从许许多多的函数集合中找到对应的函数（这些函数的集合是很泛的）。那么可以把成本函数看成是一个functional泛函数: A functional is a mapping from functions to real numbers.这个就很高级了，学习不再是调参，而是寻找函数，我们可以令损失函数的最低点为一个我们想要的函数。比如我们可以令损失函数的最低点落在一个把x映射到y的expected value的函数上。这种优化问题被称为：Calculus of variation

• 根据变分法，其实上面6.14的公式也很好看懂，也就是通过求解这个最优问题（以minimize f为目标）来找到一个计算y的均值的式子。而得出来的计算平均值的函数属于：mean absolute error

6.2.2 Output Units

• 损失函数和表示output unit的选择是深深耦合在一起的。
• 事实上，output unit和hidden unit作为神经网络的unit其实是没什么区别的，只不过output unit处于output layer并且负责output。
• 在这一个小节的学习中，hidden feature表示为：\( h = f(x;\theta) \)，而output layer则为这些特征增加了最后一层的变换

6.2.2.1 Linear Units for Gaussian Output Distribution

• 顾名思义：如果是linear unit的话，他的output layer会预测出\( \hat{y} = W^{T}h + b \)

• Linear output layers are often used to produce the mean of a conditional gaussian distribution

• 这里假设这个后验概率是高斯分布的极其重要，因为对于高斯分布的话：

  \[\begin{aligned} p(x) = \frac{1}{\sqrt{2\pi} {\sigma}} e^{-\frac{1}{2{\sigma}^{2}} x^{2}} \end{aligned}\]

• 这个性质也非常关键，可以拿来推mean square error，现在定义一个似然函数：

  \[\begin{aligned} & L(\theta) = \prod_{i = 1}^{n} p(y|x, \theta, \sigma) \\ & 给两边取对数，方便计算 \\ & J(\theta) = nln \frac{1}{\sqrt{2\pi}\sigma} - \frac{1}{2{\sigma}^{2}} \sum_{i = 1}{n}(y - f^{*}(x))^2 \end{aligned}\]
• 所以本质上，线性拟合找的是结果y的条件高斯分布的mean，然后根据最大似然的理念去得到一个代价函数，这个代价函数等同于最小二乘
• linear units do not saturate, they pose little difficulty for gradient-based optimization algorithms and may be used with a wide variety of optimizationalgorithms从不饱和，何时是个头

6.2.2.2 Sigmoid Units for Bernoulli Output Distribution

• 二元分类问题的的maximum likihood approach就是要定义一个基于伯努利分布的条件概率
• sigmoid的意义是：把线性结果转换为一个概率
• 伯努利分布指的是对于随机变量X有, 参数为p(0<p<1)，如果它分别以概率p和1-p取1和0为值。EX= p,DX=p(1-p)。伯努利试验成功的次数服从伯努利分布,参数p是试验成功的概率。伯努利分布是一个离散型机率分布，是N=1时二项分布的特殊情况，为纪念瑞士科学家詹姆斯·伯努利(Jacob Bernoulli 或James Bernoulli)而命名。
• 如果用这一个的话，因为probability需要定义在[0, 1]这个范围内，所以如果是用linear的话，如果approximate出来的东西的梯度会变成0（具体可以看书上的例子），这样子梯度是0的东西就无法对他的参数进行调整
• 综上，我们用sigmoid output unit来代替linear output unit：\( \hat{y} = \sigma (w^{T}h + b) \), 在原有的linear output的基础上多加一个sigmoid函数去把linear output z变成一个概率
• 然后书上propose了一个推理过程（how to define aprobability distribution overyusing the value z）：
  • 假设存在一个没有normalized（没有把数据映射到[0, 1]）的概率分布 \( \hat{P}(y) \)
  • 再假设这个概率分布取对数之后是和y和z成线性关系：\( log \hat{P}(y) = yz \)
  • 分别取e，消除ln：\( \hat{P}(y) = exp(yz) \)
  • 重新normalize，把这个概率变成一个恰当的概率分布：\( P(y) = \frac{exp(yz)}{\sum_{y’ = 0}^{1} exp(y’z)} \)
  • 观察发现这不就是先linear output再取sigmoid嘛！

• The z variable defining such a distribution over binary variables is called a logit

  

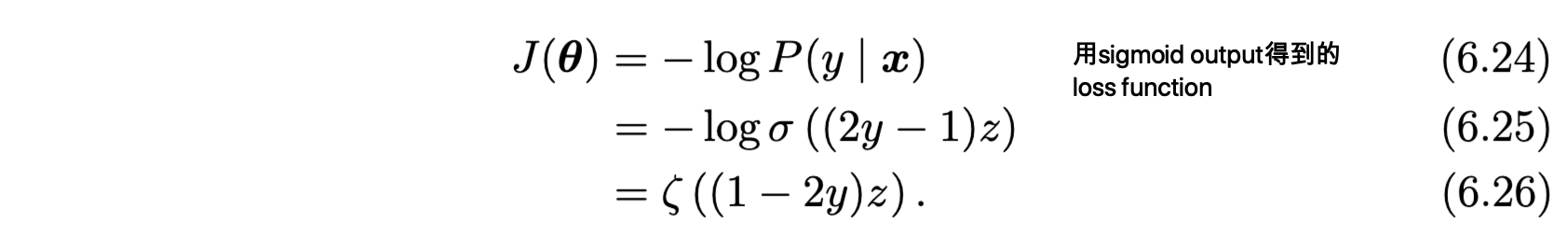
• 最后是一个softplus function，softplus function的定义如下：

• 这个的好处是在训练的时候，只有当(1-2y)z非常负->也就是点那个y = 1然后z非常正，也就是正确答案的时候，此训练才会饱和
• 那如果是一个很错误的预测呢？-> The derivative with respect tozasymptotes tosign(z), so, in the limit of extremelyincorrectz, the softplus function does not shrink the gradient at all. This propertyis useful because it means that gradient-based learning can act to quickly correcta mistaken z.
• 还是那句话，因为有sigmoid的存在，函数有时候太容易饱和了，所以两边取个对数就舒服很多

Softmax Units for Multinouli Output Distributions

• 以下定义的就是一个softmax的函数，这个函数的意义在于：可以帮助我们表示n个离散变量的概率分布

• Softmax functions are most often used as the output of a classifier, to representthe probability distribution overndifferent classes

• 和上面sigmoid的推导很像：

  • 令\( \hat{y} = P(y = i

    x) \)，并且令这个概率是一个严格的概率分布

  • 那么现在模型的目的就是求得这个hat y
  • 令linear output: \( z = W^{T} h + b \)
  • 和之前一样同取对数再normalize，oh~又发现了这特么就是softmax函数的定义：
  \[softmax(z)_{i} = \frac{exp(z_i)}{\sum_{j} exp(z_{j})}\]

• 然后再套一层log在softmax外面(log-likelihood原则的代价函数)，得到logsoftmax，这个的意义也是令这个有很多个exp term的东西不那么快饱和

  \[\begin{aligned} logsoftmax(z)_{i} = z_i - log \sum_{j} exp(z_j) \end{aligned}\]
• 看这样子的代价函数就非常的好，前面第一个term会令求梯度时不会太快饱和，从而让模型可以一直进行自我调整
• 第二的term的意义在于，如果现在预测出来的zj是对的，那么他就应该拥有很大的值，那么那个sum会大概等于zj，那么zi和zj因为很接近（zj是正确的），这个loss就会比较小；反之，这个loss就会返回一个比较大的loss的值

• 总的来说，非正则化的极大似然将驱动模型学习驱动softmax的参数，以预测在训练集中观察到的每个结果的计数的分数
• 总算来了！！从神经科学的角度来解释：softmax激起不同的神经元的竞争，因为概率总值为1，某个神经元的输出的提高, 必定意味着另一个神经元的输出变低

6.2.2.4 Other Output Types

• 总结一下，如果我们的条件概率分布是p的话，利用最大似然原则去-logp就可以知道他的代价函数

• 我们可以这么去理解神经网络：神经网络输出的并不直接是预测的y值，而是y来自的概率分布的参数w，所以代价函数如上定义
• that gradient-based optimization of conditional Gaussianmixtures (on the output of neural networks) can be unreliable, in part because onegets divisions (by the variance) which can be numerically unstable (when somevariance gets to be small for a particular example, yielding very large gradients)对混合条件高斯基于梯度的优化可能是不可靠的，因为涉及到除法的式子（当某个方差对于特定的样本变得非常小的时候，会导致非常大的梯度）-> Clip gradient/scale the gradients heuristically
• 差不多懂了，高斯混合输出是一个可以用来表示在总体分布下含有k个子分布的概率模型，高斯混合模型下有k个单高斯模型组合而成的模型，比如要预测一个东西是不是狗，这个狗的数据集的样本有体型，颜色，长相等，他们混在了一起但都属于这个狗的数据，所以对于不同的样本（颜色，体型或者长相），高斯混合模型习得一个高斯分布的参数，最后预测概率的时候把这些分别的子分布拢起来

6.3 Hidden Units

• 现在我们转向一个前馈神经网络独有的问题：该如何选择隐藏单元的类型，这些隐藏单元用在模型的隐藏层中。
• 一般使用的隐藏单元是线性整流函数\( f(x) = max(0, x) \)，这个函数的问题是他在x = 0的时候不可微，这不是基本宣告了基于梯度的学习算法无效？不过事实上，神经网络算法通常无法达到代价函数的局部最小值，根本就到不了0，所以也不用x=0
• 并且：即使导数没产生：神经网络训练的软件实现通常返回左导数或右导数的其中一个，而不是报告导数未定义或产生一个错误。当一个函数被要求计算x=0的情况时，输入的x可能是一个被舍入为0的极小的值
• most hidden units can be described as acceptinga vector of inputsx, computing an affine transformation z=Wx+b, andthen applying an element-wise nonlinear functiong(z)

6.3.1 Rectified Linear Units and Their Generalization整流线性单元及其拓展

• 就是上面描述的整流线性单元：\( g(z) = max(0, z) \)
• 好处就是，整流线性单元在其一般的定义域输出为0，这使得只要整流线性单元属于激活状态，他的梯度都能保持较大且一致：在一阶导数上处处为1
• 作用在一个仿射变化上：\( h = g(W^{T}x + b) \), 所以如果一开始就把b定义成0.1的话，可能从训练的一开始整流线性单元就对大多数的输入都呈现激活状态->允许导数通过
• Generalization of ReLu（对于普通整流函数的拓展，解决梯度方法对于激活为零的样本无用的问题）

• 在z<0时，其中alpha是非负斜率

  • Absolute value rectification：固定 αi = −1 来得到 g(z) = |z|，它的意义：用于图像中的对象识别 (Jarrett et al., 2009a)，其中寻找在输入照明极性反转下不变的特征是有意义的。

  • Leaky ReLU：fixes αi to a small value like 0.01

  • Parametric ReLU/PReLU：treats αi as a learnable parameter

• maxout unit：把z划分为每组具有k个值的组，每个maxout单元输出每组中的最大元素：

  \[g(z)_{i} = max_{j\in G^{(i)}} z_{j}\]
• 学习对输入 x 空间中多个方向响应的分段线性函数。
• 特别地，具有两块的 maxout 层可以学习实现和传统层相同的输入 x 的函数，这些传统层可以使用整流线性激活函数、绝对值整流、渗漏整流线性单元 或参数化整流线性单元，或者可以学习实现与这些都不同的函数
• maxout也需要嵌套权重
• catastrophic forgetting：neural networks forget how to perform tasks that they were trained on in the past

6.3.2 Logistic Sigmoid and Hyperbolic

• 在神经网络引入之前一般使用sigmoid函数\( g(z) = \sigma (z) \)或者是双曲正切函数（Hyperbolic Tangent）：\( g(z) = tanh(z) = \frac{cosh(z)}{sinh(z)} = 2\sigma(2z) - 1 \)
• 使用这个的问题是：sigmoid作为单元太容易饱和，只有当z非常接近于0时，才会输出敏感的梯度

6.3.3 其他隐藏单元

• 很多种类的可微函数都表现的很好。神他妈cos()的误差率小于1%
• 单位函数作为激活函数（纯线性变换）：这是以将线性变换约束为低秩的代价来实现的，但这些低秩关系往往是足够的。线性隐藏单元因此提供了一种减少网络中参数数量的有效方法。
• 其他的隐藏单元：
  • Radial Basis Function（RBF）：径向基函数，以x距离模版w的距离作为input，离得越近，越活跃
  • softmax
  • softplus：\( g(a) = log(1 + e^{a}) \)
  • hard tanh硬双曲正切函数：\( g(a) = max(-1, min(1, a)) \)

6.4 Architecture Design

• Architecture值得是指网络的整体结构：它应该具有多少单元，以及这些单元应该如何连接。
• 就好像之前记的，神经网络被组织成层的单元组。每一层都是前一层的函数
• 设计主要指的是要计算各层的宽度和整体的深度，有的时候的神经网络不需要太多层，一层也不需要太宽，便可以达到目标，但是这也让他们更难优化

6.4.1 Universal Approximation Properties and Depth

• 使用线性模型，许多损失函数会导出凸优化问题->那不就稳了！！！但问题是很多模型不是线性模型
• Universal Approximation theorem（万能近似定理）：一个前馈神经网络如果具有线性输出层和至少一层具有任何一种 ‘‘挤压’’ 性质的激活函数（例如loistic sigmoid激活函数）的隐藏层，只要给予网络足够数量的隐藏单元，它可以以任意的精度来近似任何从一个有限维空间到另一个有限维空间的 Borel 可测函数。（留个坑好吧，想知道这东西是怎么证明的）
• a feedforward network with a linear outputlayer and at least one hidden layer with any “squashing” activation function (suchas the logistic sigmoid activation function) can approximate any Borel measurablefunction from one finite-dimensional space to another with any desired nonzeroamount of error, provided that the network is given enough hidden units.
• 注意了，被逼近的函数必然是定义在有限闭区间的实值连续函数
• 这个定理代表：只要一个大的MLP，一定可以表示这个函数，但却无法保证训练算法能够学到这个函数
• no free lunch theorem shows that there is no universally superior machine learning algorithm. There is no universal procedure for examining a training set ofspecific examples and choosing a function that will generalize to points not in thetraining set
• 上面这个定理证明了只要单层神经网络足够的宽，就可以逼近任何闭区间的实值连续函数。但是这个宽度非常大（n的指数级），所以使用更深但窄的模型可以减少所需的单元数量，并且可以减少泛化误差
• 指出一些用深度整流网络表示的函数可能需要浅层网络（一个隐藏层）指数级的隐藏单元才能表示。
• Choosing a deep model encodes a very general belief that the function wewant to learn should involve composition of several simpler functions.其实在选择深层模型的时候，我们就假定了我们想要学得的函数是基于一些简单函数的组合
• 根据经验，更深的模型似乎确实在广泛的任务中泛化得更好。很可惜的是却没有证明出来

6.5.2 Other Architectural Consideration

• 虽然这里介绍的神经网络把层都以简单链式结构来描述，但并不往往是这样的。比如卷积，比如RNN，实际上，层与层之间也不用紧密相连，比如存在skip connection（These skip connections make it easier for the gradient to flow fromoutput layers to layers nearer the input.）
• 还有一个考量的是层和层之间要连接的话会怎么连接，之前看到过的是矩阵W的线性变化：每个输入单元连接到各个输出单元，但也存在每个输入单元连接到输出单元的子集，

6.5 Back-Propagation and Other Differentiation Algorithm

• 前向传播指的是从输入一层传向另一层，直到输出一个结果y。反向传播指的则是从输出层得到结果产生标量代价函数的结果，再把这个结果传回来，向后流动以便计算各层参数的调整梯度
• 关于反向传播的几个经常被误解的点：
  • 首先，反向传播仅限于计算梯度，而根据梯度调整则是：随机梯度下降
  • 反向传播不仅仅适用于MLP，它适用于计算任何函数的导数
  • 梯度的表示：\( \nabla_{x}f(x, y) \)：这个代表的是函数f关于x的梯度，我们最常需要的是代价函数关于参数的梯度: \( \nabla_{\theta}J(\theta) \)

6.5.1 Computational Graphs

• Inside the graph:
  • Node: indicate a variable(maybe a scalar, vector, matrix, tensor, or even a variable of another type)
  • “Operation”: 就是一个或多个变量的简单函数，一个operation仅返还一个值

• 更具体的：If a variable y is computed by applying an operation to a variable x, thenwe draw a directed edge from x to y.

  

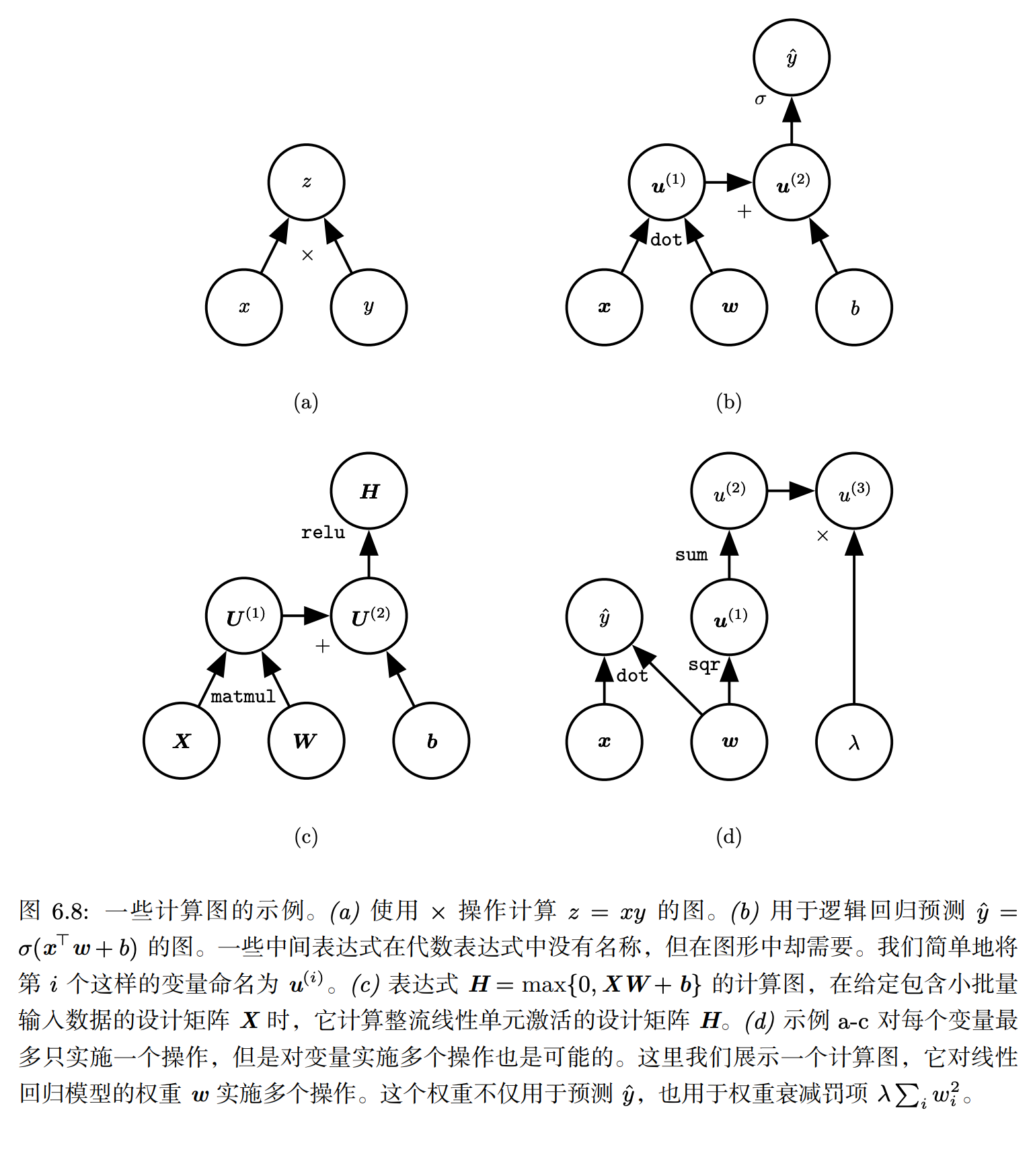
6.5.2 Chain Rule of Calculus

• 这个我真的很不想记笔记了，但是还是要记。。
• 如果\( y = g(x) \)和\( z = f(g(x)) = f(y) \)，那么：

• 上面讲到的Jacobin矩阵（雅可比矩阵）：

  

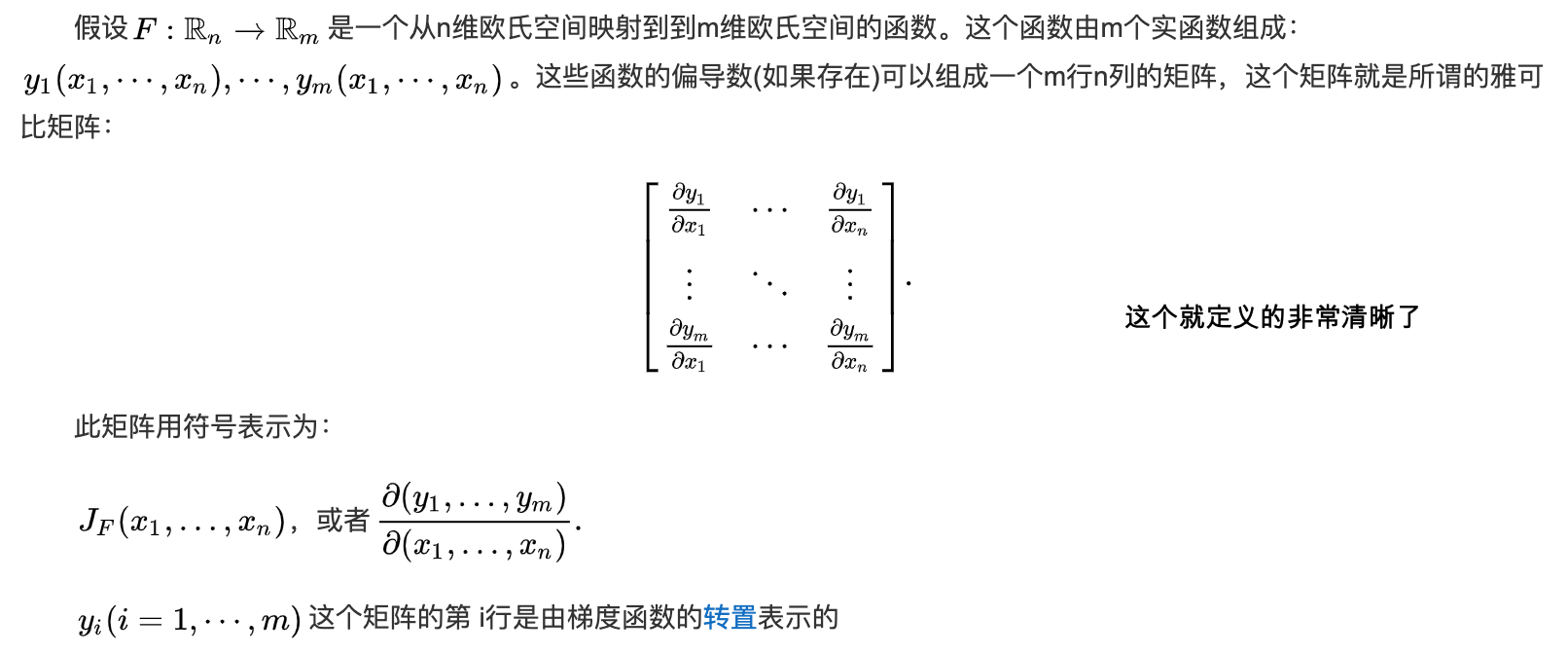
• 根据这本书自己的解释：张量值得就是超过二维的数组，一般地，一个数组中的元素分布在若干维坐标的规则网络中，我们称之为张量。张量A中坐标为(i, j, k)的元素记作\( A_{i, j, k} \)，在tensorflow中，张量tensor指的是N维数组
• 这篇博客解释的很清楚张量，矩阵和向量的区别
• 所以比如一个\( 3 \times 1908 \times 1080 \)的矩阵便是一个张量，几何上面可以想像成一个立方体。反向传播算法完全可以应用于任意维度的张量，

6.5.3 Recursively Applying the Chain Rule to Obtain Backprop

• 设计这个算法的时候可以聪明点，因为要对应许多的i点来求梯度，但这些式子很多都是重复的，为了提高效率，下面用到了dp算法去提高效率

• 执行反向传播所需的计算量与G中的边的数量成比例

6.5.4 Back-Propagation Computation in Fully connected MLP

• 前向传播和代价函数的计算就不写了，这个东西没什么含量，下面包含的是反向传播以及计算图

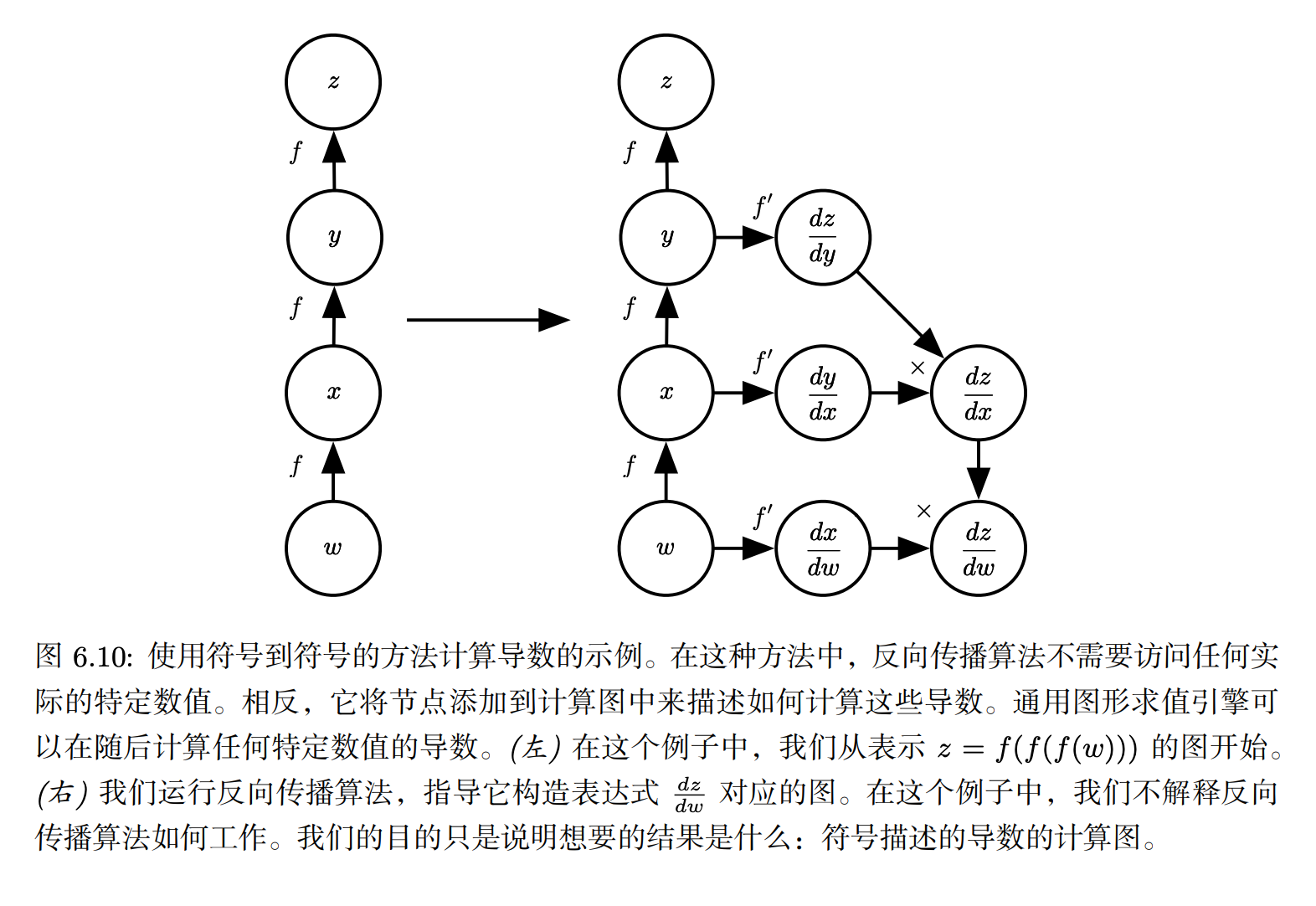
Symbol-to-Symbol Derivatives

• Some approaches to bp take a computational graph and a set of numerical values describing the gradient at those input values. 这就是Symbol to number differentiation
• 说实话我是真的没有明白这个概念的意义，反正就是可以利用很多种方法来表示梯度的计算
• 还有是符号到符号的计算方法，主要有点是导数只是另外一张计算图
• 有两种不同的编码方式：
  • 符号到数字：使用者只知道大概的网络结构，不知道具体的梯度是怎么计算的
  • 符号到符号：具体的梯度计算也被符号表示了出来

6.5.6 General Back-Propagation

• 在实际的计算图中为了最大化一般化，我们将节点对应的变量描述成一个张量（张量可以用任意维度，并且包含标量，向量和矩阵）
• 然后他这里定义了几个子程序，虽然我觉得这个定义应该都是因人而异的？
  • get_operation(V): 返回计算V的操作
  • get_consumers(V, G): 返回一组变量，计算G中V的字节点
  • get_inputs(V, G): 返回一组变量，计算G中V的父节点

• 每个操作与bprop操作相关联，bprob操作可以计算雅各布向量积

  \[op.bprop(inputs, X, G) = \sum_{i} (\nabla_{x} op.f(inputs)_{i})G_{i}\]

• 上面这个：这里，inputs 是提供给操作的一组输入，op.f 是操作实现的数学函数，X 是输入，我们想要计算关于它的梯度，G 是操作对于输出的梯度。

• 这个操作应该总是假装他的输入彼此不同：。例如，如果 mul 操作传递两个 x 来计算 x^(2)，op.bprop 方法应该仍然返回 x 作为对于两个输入的导数。反向传播算法后面会将这些变量加起来获得 2x，这是 x 上总的正确的导数。

• 在计算复杂度的时候，我们把这个算法里面的每一个operation看作是最小的单位，也就是o(1)，其他的复杂度都是根据这个为基础的，其实这个有点作弊，因为这个不是根据底层硬件的执行的单独操作，但其实这个operation又是高度可变的->比如两个多维矩阵相乘

6.5.7 Example: Back-Propagation for MLP Training

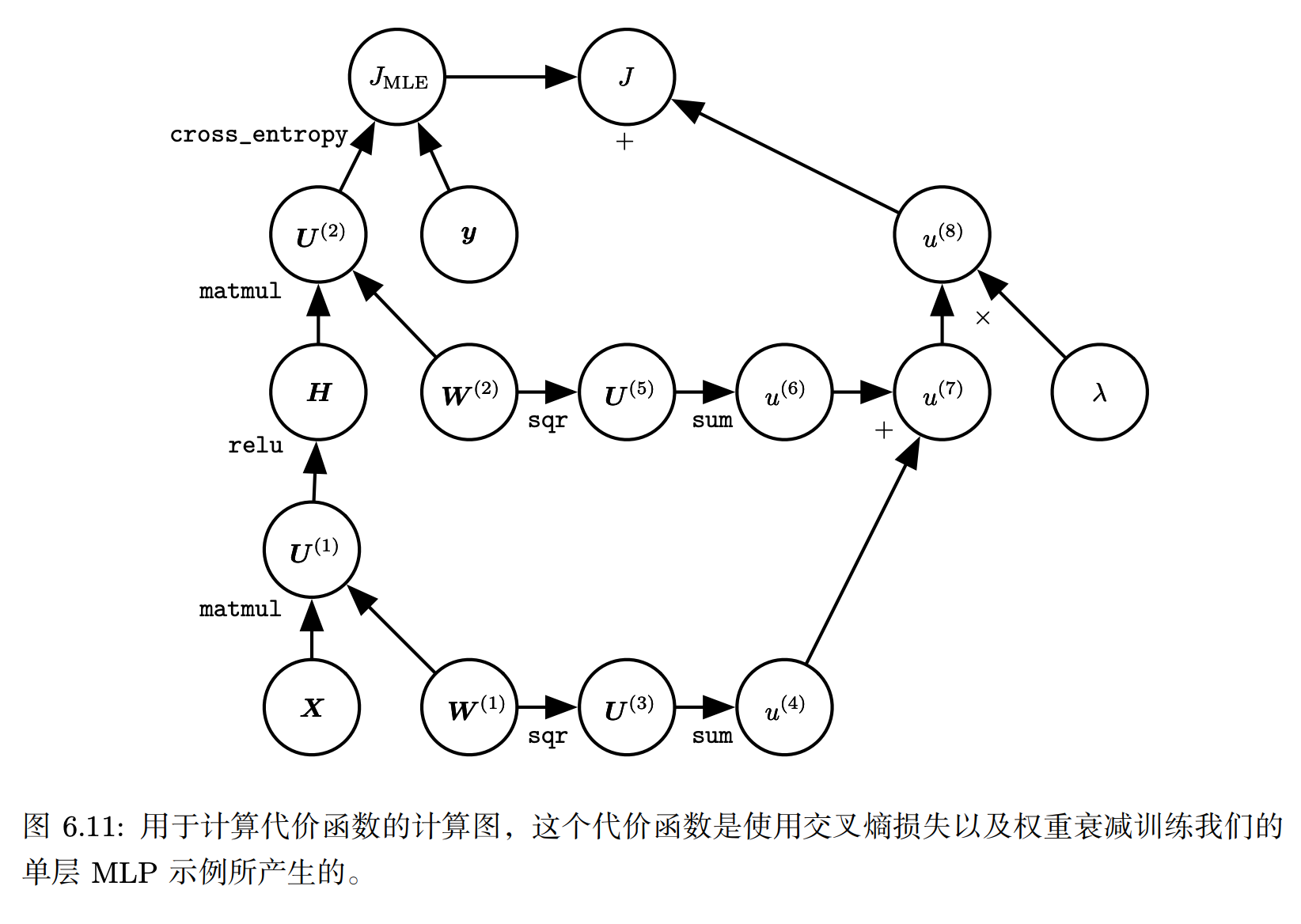
• 观察上图，对于反向传播：有两种不同的路径从 J 后退到权重：一条通过交叉熵代价，另一条通过权重衰减代价。
  • 权重衰减代价相对简单，它总是对 W(i) 上的梯度贡献 2λW(i)。

  

  而上面则介绍了反向传播从Jmle这一边应该如何传播到具体的节点

• 如果只是对于mlp来说，计算的主要成本来源于矩阵乘法。

6.5.8 Complications

• 在这里定义的反向传播算法比实际使用的实现要简单
• 比如在现实生活中，往往需要处理返还多个张量的情况
• 也没有考虑反向传播的内存消耗，最普通的办法是分别计算张量中的每一个，然后在第二步对这些张量求和。但他有过高的存储瓶颈，可以通过保持一个缓冲期，并在计算时将每个值加到该缓冲器来避免该瓶颈
• 各种其他技术的特性使现实世界的微分更加复杂。这些技术性并不是不可逾越的，本章已经描述了计算微分所需的关键知识工具，但重要的是要知道还有许多的精妙之处存在。

6.5.9 Differentiation outside the Deep Learning Communit

• Automatic Differentation(计算机领域的一种：自动微分)：领域关心如何以算法方式计算导数，在这里面描述的bp只不过是一种自动微分的方法（reverse mode accumulation）

• 惊讶！Finding the optimal sequence of operations to compute the gradient is NP-complete
• 这个问题还是个现存的很困难的问题，因为对于一些明显的表达式，人类数学家可以马上通过经验察觉出他的简单的微分形式，但bp算法无法使用这种方式来简化梯度，而是会通过原始的计算显式的传播梯度
• The overall computation isthereforeO(# edges). （for bp）
• 诸如 Theano 和 TensorFlow 的实现使用基于匹配已知简化模式的试探法，以便重复地尝试去简化图。（用到了heuristic）
• 当图的输出数目大于输入的数目时，有时更偏向于使用另外一种形式的自动微分，称为 前向模式累加（forward mode accumulation）。前向模式计算已经被提出用于循环神经网络梯度的实时计算

6.5.10 Higher-Order Derivatives

• 一些软件框架支持使用高阶导数.
• In mathematics, the Hessian matrix or Hessian is a square matrix of second-order partial derivatives of a scalar-valued function, or scalar field.
• 一般我们对hessian矩阵的性质比较感兴趣，但有时候hessian矩阵的大小很容易达到数十亿
• 虽然计算 Hessian 通常是不可取的，但是可以使用 Hessian 向量积。可以对所有的 i = 1, . . . , n 简单地计算 He(i)，其中 e(i) 是 e(i)i = 1 并其他元素都为 0的one-hot向量。

6.6 Historical Notes

• 前馈网络可以被视为一种高效的非线性函数近似器，它以使用梯度下降来最小化函数近似误差为基础。
• 神经网络这个行业已经整整快三十年没有什么显然的进步了
• 之前整流线性函数并没有流行的原因由于有些迷信的观念，认为必须避免具有不可导点的激活函数
• 从生物学考虑整流线性单元的导出。半整流非线性旨在描述生物神经元的这些性质：(1) 对于某些输入，生物神经元是完全不活跃的。(2) 对于某些输入，生物神经元的输出和它的输入成比例。(3) 大多数时间，生物神经元是在它们不活跃的状态下进行操作（即它们应该具有 稀疏激活（sparse activation））。